мои методические разработки
к.х.н. Некрасов Александр Григорьевич,
учитель физики
ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА НА ОСНОВЕ ДЕМОНСТРАЦИИ
«Моделирование опыта Штерна»
Цель опыта: Изучение кинематических закономерностей движения тела в неинерциальной системе отсчета.
Задачи демонстрационного опыта:
Образовательная: изучить данное явление и описать его математически. Получить уравнение спирали Архимеда.
Воспитательная: подчеркнуть взаимосвязь физического явления и его математическим описанием как проявления одного из признаков метода познания явлений. Продолжить работу по развитию самостоятельности, аккуратности и внимания учащихся.
Развивающая: Продолжить работу по развитию внимания и умения творчески мыслить. Научиться строить графики и получать на их основе информацию о движении тела.
Прививать навыки решения задач.
Опыт проводится на оборудовании Лаборатории L - микро «Вращательное движение».
Оборудование, подготовка установки и выполнение опыта не приводим, т. к. есть подробное описание в руководстве по выполнению эксперимента.
Теоретическое описание опыта
Пусть тело летит над вращающимся с угловой скоростью диском. Точка вылета тела совпадает с осью вращения, а скорость вылета vг направлена по радиусу диска горизонтально. В горизонтальном направлении ускорения нет, поэтому . Время движения тела для текущего значения r(t) равно
t = r / vг. (1)
За это время диск повернется на угол
φ = ωt = ωr / vг. (2)
Из формулы (2) можно определить скорость тела (в опыте Штерна это скорость молекул или атомов). Приближенно эту скорость можно определить по формуле
vг = √2gh. (3)
Где h - высота точки вылета тела над плоскостью диска. Кстати, можно сравнить скорости, найденные по формулам (2) и (3). Свяжем систему отсчета с вращающимся диском, тогда положение тела можно задать текущим значением радиуса и углом поворота . Для этих координат справедливы соотношения
r = vгt
φ = - ωt. (4)
Физический смысл знака " - " в том, что в системе координат, связанной с диском, смещение тела происходит в сторону, противоположную вращению диска. Кривая, описываемая уравнениями (4), имеет вид спирали и в математике называется спиралью Архимеда. Которая в полярной системе координат имеет вид
φ = - ωr / vг = ar.
Перейдем от полярной системы координат к декартовой c учетом r = vгt, имеем
x = r cos ωt
y = r sin ωt,
или, c учетом r = vг t получим
x = vгt cos ωt
y = vгt sin ωt,
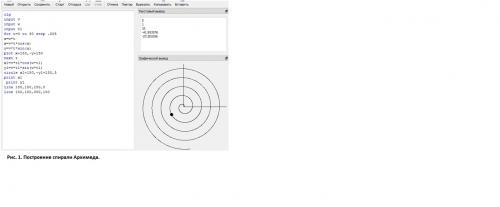
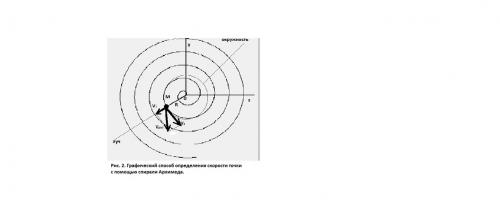
На рис. 1 приведена программа расчета в бейсик 256 и график спирали Архимеда. Точкой показано положение тела в данный момент времени. В текстовом выводе показаны скорость, угловая скорость и время наблюдения. Далее идут координаты (сначала х, затем у) тела. Для нахождения скорости тела в данной точке этот рисунок можно увеличить, как показано на рис. 2. На этом рисунке в точке М необходимо провести касательную к спирали Архимеда. Для чего через эту точку проведем окружность и луч и отложим на касательной к окружности и на луче векторы, длины которых равны линейным скоростям вращательного и поступательного движений тела. Складывая получившиеся векторы, получим вектор скорости тела, движущегося по спирали. Направление этого вектора указывает, куда направлена касательная, а его длина показывает, с какой скоростью тело движется по спирали. В практической части именно это и надо сделать. Полученное значение скорости сравнить со скоростью, рассчитанной по формуле
vрез = √v2г + (ωt)2 . (5)
На демонстрационной установке необходимо измерить радиус, угол отклонения тела . Из формулы (4) определить угловую скорость , по формуле (3) рассчитать скорость . Полученные значения ввести в программу и получить спираль Архимеда, котороу изложенным выше способом найти скорость тела.
Создано на конструкторе сайтов Okis при поддержке Flexsmm - накрутка телеграмм