nekras.okis.ru

Перед Вами примеры задач по физике повышенной трудности, уровня «С6» ЕГЭ. Задачи взяты из задачника: Задачи по физике: Учеб. Пособие . И. И. Воробьев, П. И. Зубков, Г. А. Кутузова, и др.: Под ред. О. Я. Савченко. 3-е изд.: испр. И доп. Новосибирск: Новосибирский государственный университет. 1999. 370 с..

 

 

 

 

К сожалению, решений в этом задачнике нет и я представил свои варианты решения, которые могут отличаться от составителей задач. Более того, я допускаю, что некоторые задачи могут содержать неточности. Найдите их, дорогой читатель или представьте другие способы решения. Т.е. отнеситесь творчески. А главное, набирайтесь опыта и подходов в решении задач столь высокого (олимпиадного) уровня, особенно в задачах со звездочкой. Это очень полезно при подготовке к ЕГЭ по физике в решении задач С.

            Учащийся-физик, если ты с легкостью разобрал эти задачи, то ты верно выбрал свой путь.

            Учащийся, изучающий физику в силу необходимости для получения сертификата, то эти задачи помогут поднять твой уровень и получить максимальный балл.

            Коллега, не суди строго, попробуй сам порешать задачи из этого задачника.

            Учащийся, если тебе не нужна физика, то можешь не читать.

Всем вам успеха. 

Задача1.                                                       

            В масс-пролетном спектрометре источник испускает сгусток заряженных частиц, которые сначала летят свободно и пролетают через первый датчик D₁, находящийся на расстоянии L от сетки. За сеткой по нормали к ней на частицы действует электрическая сила F. Частицы поворачиваются и вылетают через сетку назад, пролетая через второй датчик D₂, находящийся на том же расстоянии от сетки. От напряжения источника зависит скорость вылетающих частиц, но точное ее значение остается неизвестным. Меняя напряжение, измеряют время между срабатываниями датчиков и находят наименьшее его значение . Какова масса частицы?     

Ответ: t=FΔt²/16L Нужно построить по экспериментальным данным график зависимости времени пролета от напряжения источника.

            Прочитав этот ответ, меня зациклило. Где взять данные для построения графика? Тем не менее задачу можно решить стандартно, с использованием нахождения экстремума, что подробно разбирается в 11 классе. Рассмотрим рисунок: 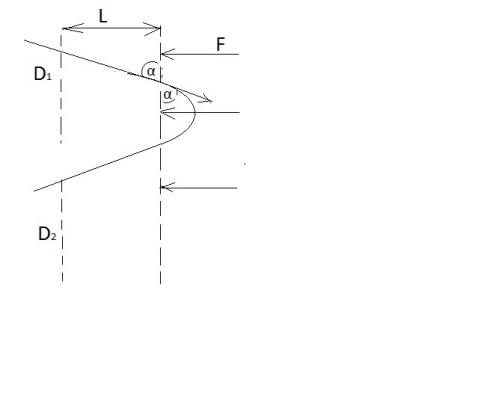                                                                                  Найдем время свободного полета частицы от D1 до сетки и от сетки до D2. Длина траектории на этом участке 2L/sinα, тогда

  t₁=2L / (sinα ·v₀)     .             (1)

Траектория частицы после сетки парабола. По аналогии движения тела, брошенного под углом к горизонту, только вместо ускорения силы тяжести будет некоторое ускорение . Из школьного курса физики время полета по параболе равно (без вывода, надо просто вспомнить)

      t₂=2v₀sinα / a   .                       (2)

Тогда общее время полета равно сумме (1) и (2)

       Δt=t₁ + t₂ = 2L / (sin α ·v₀) + 2v₀ sin α / a              (3)

Исследуем на экстремум, для чего берем производную от  Δt по v₀

(Δt)'= - 2L/(sin α ·v₀² + 2sin α / a = 0    приравняв ее к нулю. Получим

    2sin α / a = 2L/(sin α₀² , откуда v₀² = La/sin²  α = FL/(m sin² α).     (4)

Здесь использовался закон Ньютона F = ma. Сама скорость равна

 v₀ = √aL / sin α или v₀ sin α = √aL        (5)

Подставим (5) в (3)                                    

 Δt = 2L/√aL + 2√aL/a = 4√L/√a, Δt/4 = √(L/a),

 L / a =Δt² / 16.    (6)

Из (6) находим ускорение

  a=16L/Δt²  = F /m                                 (7)

Из выражения (7) находим искомую массу частицы

    m = FΔt² /16L

Автор понимает, что такую задачу на ЕГЭ вряд ли дадут. Но кто его знает. Главное не столько решить задачу, а подходы и идеи. Быть готовым к применению элементов математики. И, наконец, автор вполне допускает, что данная задача решается проще. Поищите это решение.

 значок √ - это корень квадратный. 

 

 

Задача 4. Легкий магнит с крюком на вертикальной стальной плите остается неподвижным, пока подвешенный к нему груз не превосходит по массе m₀. Чему равна магнитная сила, если коэффициент трения магнита по стали равен μ? С каким ускорением скользит магнитная подвеска, если масса груза m>m₀?                                                                         

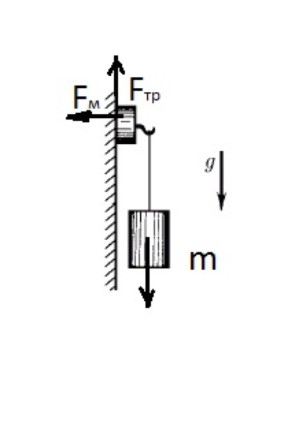   Расставим силы: Fм- магнитная  сила, Fтр - сила трения скольжения, mg - сила тяжести груза. Т.к. магнит легкий , то на него не действует сила тяжести. Условие неподвижности магнита имеет вид: m₀g = μF_м, где m₀ - масса груза, при которой начинается скольжение. Тогда магнитная сила равна F_м = m₀g / μ. Запишем второй закон Ньютона для движущегося магнита:

ma = mg - F_тр или ma = mg - m₀g . Откуда находим ускорение: a = g - m₀g/m = g(1 - m₀ / m). Исследовать полученное выражение не будем, хотя видно, что если , то скольжения не будет. Подумай почему. Замечу, что автор допустил небрежность. На самом деле на магнит также действует сила реакции опоры N и для силы трения надо писать F_тр = μN , но по третьему закону Ньютона N = F_м .

Рассмотрим еще одну простую задачу, но поучительную.

 

Задача 6. Найдите ускорение тел системы, изображенной на рисунке. Сила F приложена по направлению нити к одному из тел массы m. Участок нити по обе стороны от легкого блока, прикрепленного к телу массы М, параллельны.

 Сделаем более подробно этот рисунок, на котором укажем силы, характеризующие взаимодействие тел.                                                                                                                                 

                                                                                                                                 

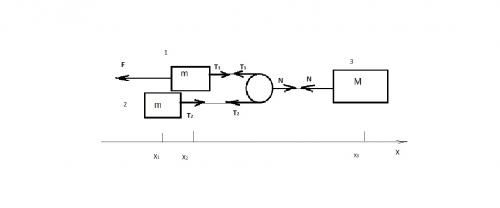
 В рамочках указаны силы. Составим уравнения движения тел:

ma₁ = F - T₁

ma₂ = T₂

m_блокаa = T₁ + T₂ - N

Ma₃ = N                           

Шесть неизвестных и 4 уравнения. Система не решается. Запишем последнее уравнение в виде

 Ma₃ = T₁ + T₂

Стало 3 уравнения и 5 неизвестных. Надо выходить из положенния. Т.е. составить еще два уравнения. Воспользуемся условием невесомости нити. Составим уравнение движения для нити.

 m_нитиa = T₂ - T₁.

Т.к. масса нити равна нулю, то T₁ = T₂. Найдем взаимосвязь между ускорениями тел. Поскольку блок подвижный, то ускорение тела M будет равно  и направлено влево. Ускорение тела 1 равно  a₁ и направлено влево, тогда как ускорение тела 2 равно  a₂ и направлено вправо. В проекциях на ось Х взаимосвязь между ускорениями тел примет вид.

a₁ - a₂ = 2a_3. Ниже это будет доказано строго.

Таким образом мы получили два новых уравнения:

T₁ = T₂  и 2a₃ = a₁ - a₂.

Тогда исходная система примет вид:

 ma₁ = F - T

 ma₂ = T

Ma₃ = 2T

2a₃ = a₁ - a₂

Вроде все нормально: 4 уравнения и 4 неизвестных. Решаем эту систему относительно ускорений. Решение этой системы кажется сложным, попрубуйте ее решить самостоятельно, в конце концов это чисто математическая задача. Вы должны получить следующие ответы

 a₃ = F / (2m + M); a₂ = FM / 2m(2m + M); a₃ = F(M + 4m) / 2m(M +2m).

Обратили внимание, что это задача со звездочкой. Напоминаю, что решение автора может отличатся от автора задачника, хотя ответы совпали. Необходимо заметить, что в приведенном решении есть какая-то недосказанность. А именно, это взаимосвязь между ускорениями. Получим эту связь строго. Рассмотрим рисунок.

 

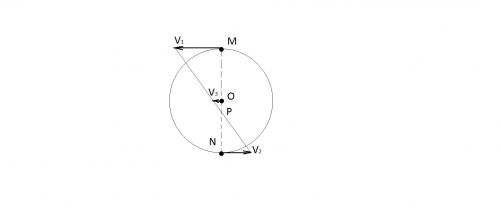
 силу нерастяжимости нити скорость тела 1 равна скорости т. М блока (проскальзывания нет), а скорость тела 2 - скорости т. N.

Пусть ОР = x, имеем v₁/v₂=MP/NP=(R+x)/(R-x), откуда нетрудно найти x=R(v₁-v₂)/(v₁+v₂).Угловая скорость блока  ω=v₁/MP=v₁/(R+x);

R+x=R+R(v₁-v₂)/(v₁+v₂)=R(1+(v₁-v₂)/(v₁+v₂))=2Rv₁/(v₁+v₂), ω=(v₁+v₂)/2R, v₃=OP·ω=(v₁-v₂)/2.

Дифференцируя, получим для ускорений: 2a₃ = a₁ - a₂. 

Просто эту формулу надо запомнить.

Другой подход. Найдем длину нити:

 L = (x₃ - x₂) + (x₃ - x₁) + l_блока = const

Дифференцируя дважды, получим взаимосвязь ускорений

 2a₃ = a₂ + a₁

А теперь надо выбрать знаки в соответствии с выбранной осью: 2a₃ = a₁ - a₂.Тоже не здорово, но все-таки более менее понятно.

 

Задача 7 На два катка разного радиуса положили тяжелую плиту. Она образует угол α с горизонтом. Найдите ускорение этой плиты. Проскальзывания нет. Массой катков пренебречь.

 

Над этой задачей пришлось подумать немалое время. Казалось, что просто, ускорение равно a = g sin α, однако, ответ дается такой: a = g sin (α / 2)

Сделаем рисунок крупнее:

  

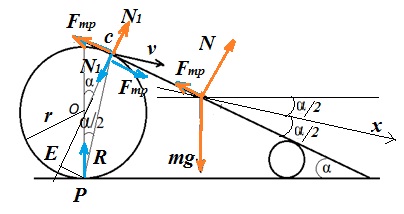
 Движение плиты сложное, состоит из горизонтального (за счет движения катков) и под углом к горизонту, и является поступательным. Расставим силы. Векторы синим цветом - это силы, действующие на каток (N₁ - сила со стороны плиты на каток/ она равна и противоположно направлена силе со стороны катка на плиту, F_тр - сила трения, действующая на каток (под ее действием происходит вращение катка), и сила реакции опоры R в точке Р). Аналогичные силы действуют на каток меньшего радиуса. Векторы красного цвета обозначают силы, действующие на плиту (N - суммарная сила реакций опор, mg - сила тяжести, F_тр - сила трения со стороны катков на плиту). Выберем ось Х по направлению скорости движения плиты. Сама же скорость это мгновенная скорость точки касания плиты и еатка, а точка Р - мгновенный центр скоростей, причем v перпендикулярна РС (мгновенный радиус вращения). Запишем в проекциях на ось Х уравнение движения плиты

ma = mg sin a/2 + N sin a/2 - F_тр сos a/2 .             (1)

В этом уравнении три неизвестных. Необходимо составить еще уравнения. Запишем уравнение вращательного движения для катка. Это уравнение имеет вид Iε = ΣM, произведение момента инерции тела на угловое ускорение равно сумме моментов сил, действующих на тело. Найдем плечи сил, действующих на каток. PC - 2r cos α / 2 . Плечо силы трения равно 2r cos α / 2 · cos α / 2, а плечо силы N равно 2r cos α / 2 · sin α/2 . Плечо силы R равно нулю. Запишем уравнение вращательного движения для катка (т.к. масса катка по условию задачи равна нулю, то и I = 0):

0 = - F_тр 2r cos α / 2 · cos α / 2 + N 2r cos α / 2 · sin α / 2.            (2)

Откуда F_тр = N tg α / 2, подставляя это значение в уравнение движения (1), получим ma = mg sin α / 2, т.е. искомое ускорение равно a = g sin α/2.  Это и есть ответ.                       

  

Задача 8. В сферическую полость поместили гантель (два шарика массы m каждый, соединенные невесомым стержнем) так, как это показано на рисунке. Определите силу давления шариков на стенки сразу же после того, как гантель отпустили. Радиус шариков гантели много меньше радиуса сферы.

 

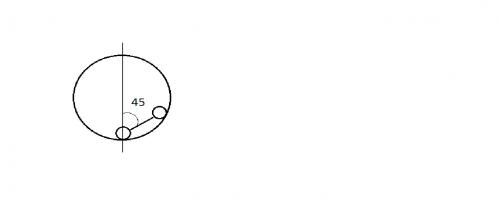
Сделаем рисунок более крупным. Расставим силы. В начальный момент гантель не движется, поэтому запишем увторой закон ньютона с учетом, что ускорение равно нулю.    Эти уравнения примут вид:

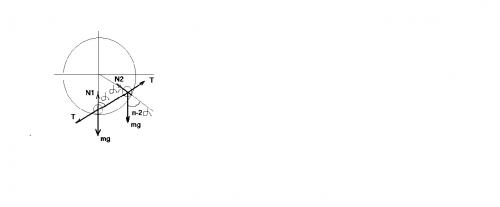
 0 = N₁ - mg - Tcos α

0 = N₂ - mg cos(π - 2α) + Tcos α. Нетрудно догадаться, что проектирование велось по направлениям N₁ и N₂. Из этой системы находим

N₁ - N₂ = 2mg

N₁ + N₂ = mg - mg cos(π - 2α) , т.к. cos(π - 2α) = cos2α, то N₁ + N₂ = mg - mg cos2α. По условию задачи α =90⁰ . С учетом этого окончательно получим

 N₁ = 3mg,  N₂ = -mg / 2.  Знак " - " означает, что сила направлена в противоположную сторону, как указано на рисунке.